こんにちは!
物理を学ぶ上で避けて通れないのが、「座標系」です。
この記事では、まず、2次元座標系のうち、特に重要な次の2つの座標系について説明します。
- 2次元直交座標系(デカルト座標、カーテシアン座標とも言う)
- 2次元極座標系
その後、なぜ座標系を導入する必要があるのかを説明します!
2次元直交座標系
まず、2次元直交座標系について説明します。
これは最も基本的なものなので、しっかり理解しておきましょう!
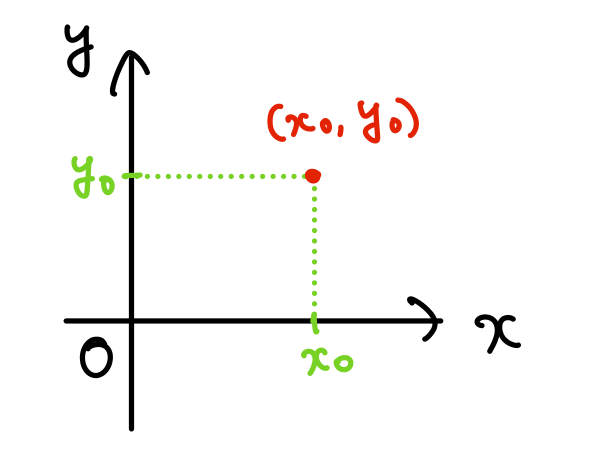
上図のように、互いに直交する座標軸(\(x \)軸と\(y \)軸)によって座標を決定します。
この図では、原点Oから\(x=x_0\)、\(y=y_0\)だけ離れた特定の座標(位置)に点があることを示しています。
2次元極座標系
次に、2次元極座標系について説明します。
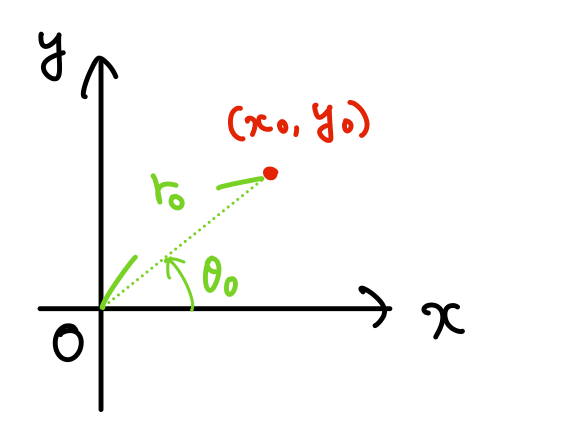
先ほどと同じ位置\((x_0,y_0)\)を、図のように原点からの距離\(r_0\)と、\(x \)軸の正の方向とのなす角\(\theta_0\)で表すことができます。
これを2次元極座標系といいます。
以降、特定の座標を表す添字\(0\)を省略します。
図より、2次元直交座標系との関係は、
\begin{align}
x=r\cos{\theta},\quad
y=r\sin{\theta}
\end{align}
となります。
ただし、それぞれの取り得る値の範囲は、
\begin{align}
-\infty<x<\infty,\quad-\infty<y<\infty \\
0\le r<\infty,\quad 0\le\theta<2\pi
\end{align}
であることに注意しましょう。これで、2次元平面のあらゆる点を過不足なく指定できます。
2次元極座標系は、円軌道を解くときに便利で、力学では中心力を扱うときなどに出てきます!
なぜ座標系を導入するのか?

最後に、なぜ座標系を導入する必要があるのかについて考えてみます。
例えば、家族がペンを探しているとき、あなたが「そこにあるよ(^^)」と伝えるとします。
目線で伝えたりやジェスチャーをしなかった場合、「そこってどこ?!(`ε´)」とおそらくペンの場所は伝わらないでしょう。
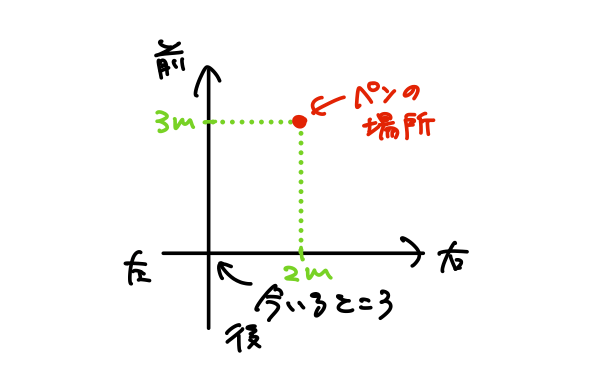
しかし、「今いるところから、右に2m、前に3mだけ移動したところにあるよ(^^)」と伝えたらどうでしょう。
ペンの場所にたどり着けるはずです。
なぜでしょう。
それは、あなたが①基準(=今いるところ)と②座標軸(=左右、前後)を設定し、それをもとに場所を伝えたので、家族にきちん伝わったからです。
これから質点の運動など具体的な問題について扱う予定ですが、この例のように、物の位置を誰にでもわかるように指定する必要があります。
そのための手段が座標系を導入することです。
ちなみに、この例と2次元直交座標系との間には、次のような対応があります。
基準=今いるところ=原点O
座標軸=前後左右=\(x \)軸と\(y \)軸
まとめ
2次元座標系のうち、重要な2つの座標系
- 2次元直交座標系\((x,y)\)
- 2次元極座標系\((r,\theta)\)
について紹介しました。
これらの間の関係は、次のようになります。
\begin{align}
x=r\cos{\theta},\quad
y=r\sin{\theta}
\end{align}
それでは!

