こんにちは!
この記事では、2次元回転行列の導出を行います。
- 2次元回転行列の導出を知りたい
という方におすすめです(^^)
回転前後の成分の関係
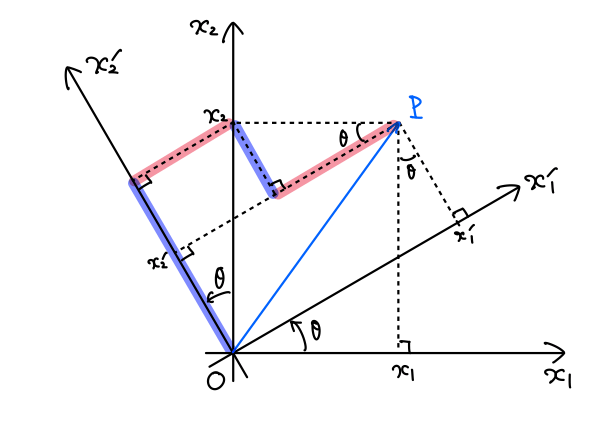
ここでは、ベクトルではなく座標軸を回転させることを考えます。
回転角を\(\theta\)とします。
回転前の座標軸を\(x_1,x_2\)、回転後の座標軸を\(x’_1,x’_2\)としましょう。
点Oから点Pまでを結ぶ位置ベクトルを考えます。
このベクトルが回転前の座標系で\((x_1,x_2)\)という成分をもつとき、回転後の成分を求めます。
まず、図の赤マーカー部分の和が\(x’_1\)に等しいので、
\begin{align}
x’_1=x_1\cos{\theta}+x_2\sin{\theta} \tag{1}
\end{align}
次に、図の青マーカー部分の差が\(x’_2\)に等しいので、
\begin{align}
x’_2=-x_1\sin{\theta}+x_2\cos{\theta} \tag{2}
\end{align}
2次元回転行列の導出
(1)、(2)を組み合わせて行列表記すると、
\begin{align}
\begin{pmatrix} x’_1 \\ x’_2 \end{pmatrix}
=\begin{pmatrix} \cos{\theta} & \sin{\theta} \\ -\sin{\theta} & \cos{\theta} \end{pmatrix}\begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \tag{3}
\end{align}
ここに現れる\(2\times2\)行列\(R(\theta)\)を2次元回転行列といいます:
\begin{align}
R(\theta)\equiv\begin{pmatrix} \cos{\theta} & \sin{\theta} \\ -\sin{\theta} & \cos{\theta} \end{pmatrix} \tag{4}
\end{align}
まとめ
この記事では、2次元回転行列の導出を行いました!
その表式は、次のようになります:
\begin{align}
R(\theta)\equiv\begin{pmatrix} \cos{\theta} & \sin{\theta} \\ -\sin{\theta} & \cos{\theta} \end{pmatrix}
\end{align}
ただし、ベクトルではなく座標系を\(\theta\)だけ回転させていることに注意しましょう。
それでは!