こんにちは!
この記事では、3次元座標系(直交座標、極座標、円柱座標)のまとめをします!
その前に2次元座標系について知りたい方はこちらをご覧ください。
早速内容に行きましょう(^^)
3次元直交座標系
3次元直交座標系では、互いに直交している3つの座標軸で座標を指定します。
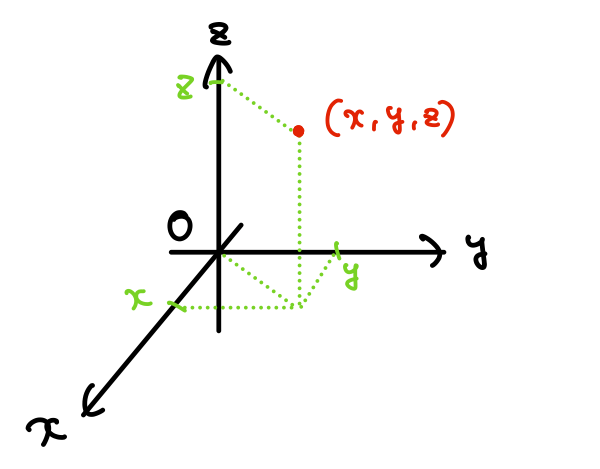
図のように、座標を\((x,y,z)\)で指定します。
それぞれの変数の取り得る値の範囲は、
\begin{align}
-\infty<x<\infty,\quad-\infty<y<\infty,\quad-\infty<z<\infty
\end{align}
です。
3次元極座標系
次に、先ほどと同じ位置を3次元極座標系\((r,\theta,\phi)\)で表しましょう。
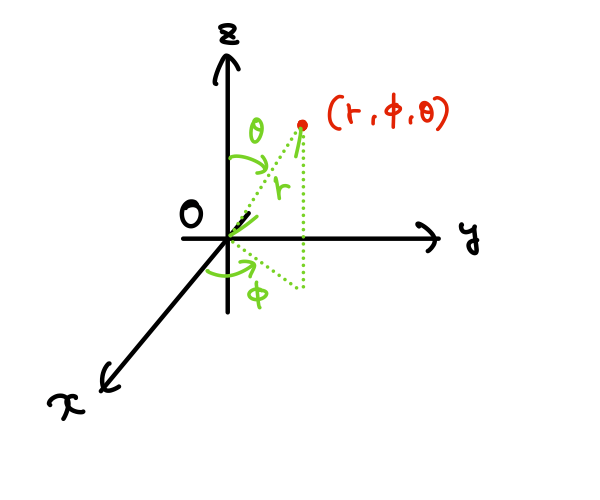
原点から座標\((x,y,z)\)に向かうベクトルを\(\boldsymbol{r}\)とすると、\(r\)、\(\theta\)、\(\phi\)はそれぞれ、
- \(r=|\boldsymbol{r}|\):原点から\((x,y,z)\)までの距離
- \(\theta\):\(\boldsymbol{r}\)と\(z \)軸の正の方向のなす角
- \(\phi\):\(\boldsymbol{r}\)を\(xy \)平面に射影したベクトルと\(x \)軸の正の方向のなす角
を表しています。
つまり、3次元直交座標系\((x,y,z)\)との関係は、
\begin{align}
x&=r\sin{\theta}\cos{\phi},\\
y&=r\sin{\theta}\sin{\phi},\\
z&=r\cos{\theta}
\end{align}
となります。
ただし、
\begin{align}
0\le r<\infty,\quad 0\le\theta\le\pi,\quad 0\le\phi<2\pi
\end{align}
で3次元空間のあらゆる点を過不足なく指定できます。
球対称な系を扱うときに便利です。
3次元円柱座標系
最後に、3次元円柱座標系\((r,\phi,z)\)を導入します。これは円筒座標系とも呼ばれます。
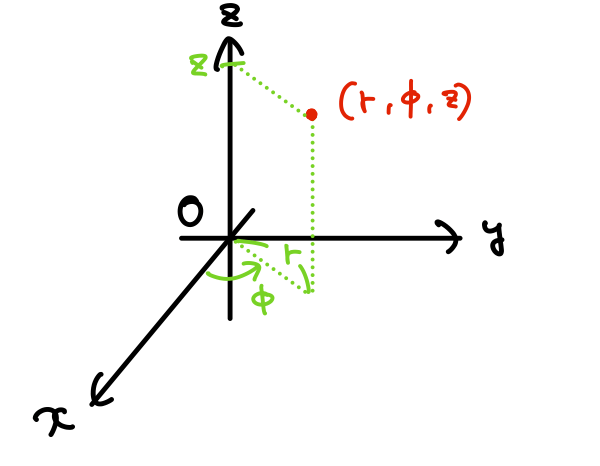
\(r\)と\(\phi\)は2次元極座標系のものと同じで、\(z\)は直交座標系のものです。(2次元極座標系についてはこちら)
2次元極座標系に加えて、高さの方向として\(z \)軸方向を考えるということです。
すなわち、3次元直交座標系との間には次のような関係があります。
\begin{align}
x&=r\cos{\phi},\\
y&=r\sin{\phi},\\
z&=z
\end{align}
ただし、
\begin{align}
0\le r<\infty,\quad 0\le\phi<2\pi,\quad -\infty<z<\infty
\end{align}
です。
らせん運動などを扱うときに便利です。
まとめ
3次元座標系として、
- 直交座標系
- 極座標系
- 円柱座標系
を紹介しました。
それでは!


