こんにちは!
この記事では、ベクトルを回転させた前後で内積が不変なことを具体的に示します。
その後、この議論を一般化して直交変換に対して内積が不変であることを証明します。
まとめでは、素粒子の理論との関わりの小話を入れておいたので、興味のある方はぜひ最後までご覧ください!(^O^)
早速内容に入りましょう!
回転行列の復習
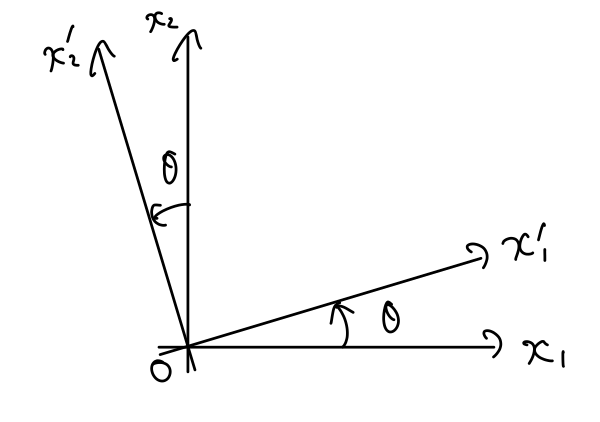
図のように、座標系を\(\theta\)だけ回転させることを考えます。
このとき、回転行列\(R(\theta)\)は次のように表されます:
\begin{align}
R(\theta)\equiv\begin{pmatrix} \cos{\theta} & \sin{\theta} \\ -\sin{\theta} & \cos{\theta} \end{pmatrix} \tag{1}
\end{align}
詳しい導出はこちらの記事をご覧ください↓
回転前後のベクトルの成分の関係
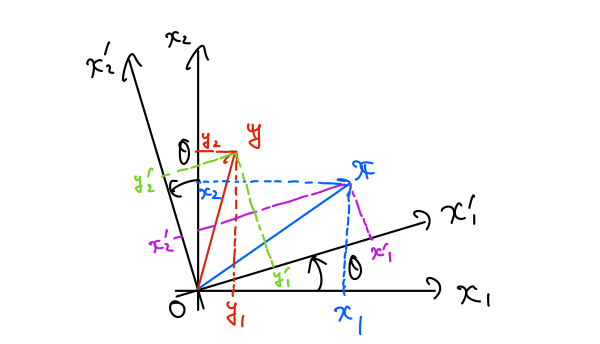
図のように、回転前の座標系のおいて2つの位置ベクトル\(\boldsymbol{x},\,\boldsymbol{y}\)を考えます。
これらのベクトルの回転前の成分を、
\begin{align}
\boldsymbol{x}=\begin{pmatrix} x_1 \\ x_2 \end{pmatrix},\quad \boldsymbol{y}=\begin{pmatrix} y_1 \\ y_2 \end{pmatrix} \tag{2}
\end{align}
とします。
回転後の座標系からみたこれらのベクトルを\(\boldsymbol{x}’,\,\boldsymbol{y}’\)とかき、それぞれの成分を、
\begin{align}
\boldsymbol{x}’=\begin{pmatrix} x’_1 \\ x’_2 \end{pmatrix},\quad \boldsymbol{y}’=\begin{pmatrix} y’_1 \\ y’_2 \end{pmatrix} \tag{3}
\end{align}
とします。(この記号\(\,{}’\)はプライムと読みます。)
プライムありとなしの座標は回転行列(1)によって次のように結ばれています:
\begin{align}
\boldsymbol{a}’&=R(\theta)\boldsymbol{a}\tag{4}\\
&\Rightarrow
\begin{cases}
a’_1=a_1\cos{\theta}+a_2\sin{\theta} \\
a’_2=-a_1\sin{\theta}+a_2\cos{\theta}
\end{cases}\tag{5}
\end{align}
ただし、\(a=x,y\)です。
内積が不変なこと
内積が不変なことを示す準備が整いました!
回転前の内積\((\boldsymbol{x},\boldsymbol{y})\)は、
\begin{align}
(\boldsymbol{x},\boldsymbol{y})\equiv x_1y_1+x_2y_2 \tag{6}
\end{align}
回転後の内積\((\boldsymbol{x}’,\boldsymbol{y}’)\)は、
\begin{align}
(\boldsymbol{x}’,\boldsymbol{y}’)\equiv x’_1y’_1+x’_2y’_2 \tag{7}
\end{align}
これに(5)を代入しましょう。
\begin{align}
(\boldsymbol{x}’,\boldsymbol{y}’)
&=x’_1y’_1+x’_2y’_2\\
&=(x_1\cos{\theta}+x_2\sin{\theta})(y_1\cos{\theta}+y_2\sin{\theta})\\
&\quad+(-x_1\sin{\theta}+x_2\cos{\theta})(-y_1\sin{\theta}+y_2\cos{\theta})\\
&=x_1y_1\cos^2{\theta}+x_1y_2\cos{\theta}\sin{\theta}+x_2y_1\sin{\theta}\cos{\theta}+x_2y_2\sin^2{\theta}\\
&\quad +x_1y_1\sin^2{\theta}-x_1y_2\cos{\theta}\sin{\theta}-x_2y_1\sin{\theta}\cos{\theta}+x_2y_2\cos^2{\theta}\\
&=x_1y_1+x_2y_2 \\
&=(\boldsymbol{x},\boldsymbol{y}) \tag{8}
\end{align}
4つ目の等号では、\(\cos^2{\theta}+\sin^2{\theta}=1\)を用いました。
これで、回転の前後で内積が不変なことがわかりました!
直交変換と内積の不変性
これまでの議論で、具体的に2次元回転行列をベクトルに作用させても内積が不変であることがわかりました。
この議論を一般化して、直交変換に対して、内積が不変なことを証明します。
直交変換
→直交行列(\(A^{\rm T}=A^{-1}\))によるベクトルの線形変換のこと
\(A^{\rm T}\)は行列\(A\)の転置行列で、\(A^{-1}\)は\(A\)の逆行列です。
回転行列は直交行列です。
なぜなら、
\begin{align}
[R(\theta)]^{\rm T}
&=\begin{pmatrix} \cos{\theta} & \sin{\theta} \\ -\sin{\theta} & \cos{\theta} \end{pmatrix}^{\rm T}\\
&=\begin{pmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{pmatrix}\\
&=\begin{pmatrix} \cos{(-\theta)} & \sin{(-\theta)} \\ -\sin{(-\theta)} & \cos{(-\theta)} \end{pmatrix}\\
&=R(-\theta)\\
&=[R(\theta)]^{-1} \tag{9}
\end{align}
となるからです。
最後の等号は、具体的に\(R(-\theta)R(\theta)=1\)となることを計算しても良いですし、\(\theta\)だけ回転させたあとに\(-\theta\)だけ回転させれば元に戻る、と直感的に理解しても良いです。
したがって、回転行列を作用させる変換は直交変換であることがわかります。
さて、内積が次のようにかけることに注意しましょう。
\begin{align}
(\boldsymbol{x},\boldsymbol{y})\equiv x_1y_1+x_2y_2=\boldsymbol{x}^{\rm T}\boldsymbol{y} \tag{10}
\end{align}
よって、回転後の内積は、
\begin{align}
(\boldsymbol{x}’,\boldsymbol{y}’)
&=\boldsymbol{x}’^{\rm T}\boldsymbol{y}’\\
&=[R(\theta)\boldsymbol{x}]^{\rm T}R(\theta)\boldsymbol{y}\\
&=\boldsymbol{x}^{\rm T}[R(\theta)]^{\rm T}R(\theta)\boldsymbol{y}\\
&=\boldsymbol{x}^{\rm T}[R(\theta)]^{-1}R(\theta)\boldsymbol{y}\\
&=\boldsymbol{x}^{\rm T}\boldsymbol{y} \tag{11}
\end{align}
3つ目の等号では、\((AB)^{\rm T}=B^{\rm T}A^{\rm T}\)を用いました。
4つ目の等号では、(9)を用いました。
(11)では、回転行列の具体的な成分を用いずに、それが直交行列であるという性質だけから内積が不変であることを示しました!
この議論は一般の直交行列に対して成り立ちます。
まとめ
この記事では、次のことを示しました。
- 2次元回転行列を作用させる前後で、ベクトルの内積が不変であること(具体的に成分を用いて)
- 一般に直交変換(直交行列を用いた変換)に対して内積が不変であること
余談ですが、物理において「不変性(対称性)」という考え方は重要です。
例えば、2024年現在までの高エネルギー実験のほとんどを説明している素粒子標準模型という理論は、ある対称性を原理として構築されています。
そういった素粒子の理論などを理解するための第一歩として、この記事でやったように回転という具体的にイメージできる変換で不変性という概念に慣れておくことは大切だと思います。
ちなみに、ここで議論した2次元回転行列の集合のことを、群論の言葉で\(SO(2)\)と呼びます。
興味のある方は調べてみてください!(^^)
それでは!


