こんにちは!
この記事では、最小作用の原理からEuler-Lagrange方程式の導出を行います。
途中計算を詳しく載せたので、
- 最小作用の原理からEuler-Lagrange方程式を導出する計算過程を知りたい
という方の参考になれば幸いです(^^)
最小作用の原理
最小作用の原理
時刻\(t_1<t<t_2\)において、一般化座標\(q(t)\)は、次の作用が極値をとるように決まります:
\begin{align}
S[q]=\int^{t_2}_{t_1} dt L(q(t),\dot{q}(t),t) \tag{1}
\end{align}
ただし、境界条件として、
\begin{align}
q(t_1)=q_1,\quad q(t_2)=q_2 \tag{2}
\end{align}
を指定します。
ただし、\(q(t)=(q_1(t),\dots,q_N(t))\)です。(\(N\)は系の自由度)
Euler-Lagrange方程式の導出
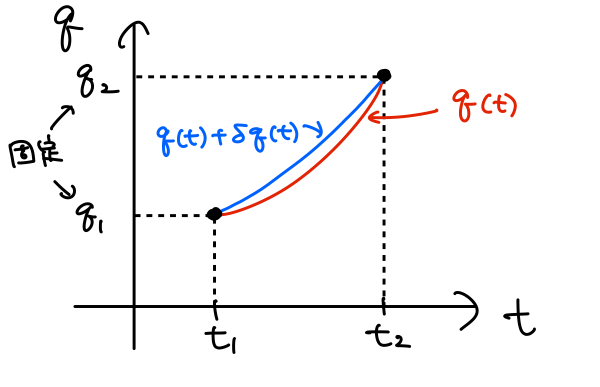
図の\(q(t)\)が、作用\(S\)が極値をとるような軌道だとしましょう。
この軌道から少しずれた任意の軌道
\begin{align}
q(t)+\delta q(t) \tag{3}
\end{align}
を考えます。
境界条件(2)より、
\begin{align}
\delta q(t_1)=\delta q(t_2)=0 \tag{4}
\end{align}
です。
これらの2つの軌道に対する作用の差\(\delta S\)(これを変分といいます)を計算します。
\begin{align}
\delta S
&=\int^{t_2}_{t_1} dt \left(L(q+\delta q,\dot{q}+\delta \dot{q},t)-L(q,\dot{q},t)\right)\\
&\simeq\int^{t_2}_{t_1} dt \left(L(q,\dot{q},t)+\frac{\partial L}{\partial q_i}\delta q_i+\frac{\partial L}{\partial \dot{q}_i}\delta \dot{q}_i-L(q,\dot{q},t)\right)\\
&=\int^{t_2}_{t_1} dt \left(\frac{\partial L}{\partial q_i}\delta q_i+\frac{\partial L}{\partial \dot{q}_i}\delta \dot{q}_i\right) \tag{5}
\end{align}
2行目では、\(L(q+\delta q,\dot{q}+\delta \dot{q},t)\)をテイラー展開をして、微小量\(\delta q_i, \delta \dot{q}_i\)の1次まで残しました。
次に、
\begin{align}
\delta \dot{q}_i=\frac{d}{dt} \delta q_i \tag{6}
\end{align}
を用いると(この変形はこちらの記事で詳しく説明しています)、
\begin{align}
\delta S=\int^{t_2}_{t_1} dt \left(\frac{\partial L}{\partial q_i}\delta q_i+\frac{\partial L}{\partial \dot{q}_i}\frac{d}{dt} \delta q_i\right) \tag{7}
\end{align}
となります。
この第2項を部分積分すると、
\begin{align}
\delta S=\int^{t_2}_{t_1} dt \left(\frac{\partial L}{\partial q_i}-\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_i}\right)\delta q_i+\left[\frac{\partial L}{\partial \dot{q}_i}\delta q_i\right]^{t=t_2}_{t=t_1} \tag{8}
\end{align}
この最後の項を表面項といいます。
(4)より、表面項はゼロになります。
よって、
\begin{align}
\delta S=\int^{t_2}_{t_1} dt \left(\frac{\partial L}{\partial q_i}-\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_i}\right)\delta q_i \tag{9}
\end{align}
作用\(S\)が極値をとる条件は\(\delta S=0\)です。
\(\delta q_i\)は任意なので、
\begin{align}
\frac{\partial L}{\partial q_i}-\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_i}=0 \tag{10}
\end{align}
であれば\(\delta S=0\)となります。
この(10)をEuler-Lagrange方程式といいます。
まとめ
この記事では、最小作用の原理からEuler-Lagrange方程式を導きました。
それでは!


