こんにちは!
この記事では、2次元極座標の基底ベクトルを解説します!
2次元極座標について知りたい方はこちらの記事もどうぞ!
2次元極座標の基底ベクトルのまとめ
2次元極座標\((r,\phi)\)の基底ベクトル
\begin{align}
\boldsymbol{e}_{r}&=\cos{\phi}\boldsymbol{e}_{x}+\sin{\phi}\boldsymbol{e}_{y}, \tag{1}\\
\boldsymbol{e}_{\phi}&=-\sin{\phi}\boldsymbol{e}_{x}+\cos{\phi}\boldsymbol{e}_{y} \tag{2}
\end{align}
下図のように、それぞれ\(r\)が増える方向、\(\phi\)が増える方向の単位ベクトルです。
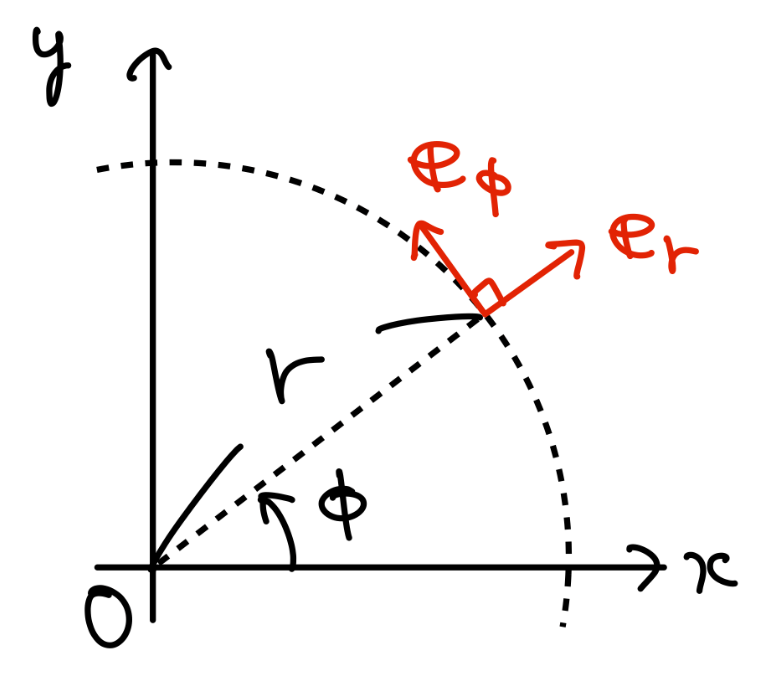
導出
基底ベクトルを導出する方法はいくつかありますが、ここでは、どのような座標系に対しても適用できる方法を採用します。
基底ベクトルの導出方法
- 位置ベクトル\(\boldsymbol{r}\)をデカルト座標の基底ベクトルで展開する
- 求める座標系の成分とデカルト座標の成分の関係を求め、代入する
- 求める座標系の成分で位置ベクトルを偏微分する
- 規格化する
この方法で、2次元極座標の基底ベクトルを求めましょう。
まず、2次元位置ベクトルをデカルト座標の基底ベクトルで展開します。
\begin{align}
\boldsymbol{r}=\boldsymbol{e}_{x}x+\boldsymbol{e}_{y}y \tag{3}
\end{align}
次に、極座標の成分とデカルト座標の成分の関係
\begin{align}
x=r\cos{\phi},\quad
y=r\sin{\phi} \tag{4}
\end{align}
を(3)に代入します。
\begin{align}
\boldsymbol{r}=\boldsymbol{e}_{x}r\cos{\phi}+\boldsymbol{e}_{y}r\sin{\phi} \tag{5}
\end{align}
そして、2次元極座標の成分\(r,\phi\)で位置ベクトル\(\boldsymbol{r}\)を偏微分します。
\(r\)で偏微分すると、
\begin{align}
\frac{\partial\boldsymbol{r}}{\partial r}=\boldsymbol{e}_{x}\cos{\phi}+\boldsymbol{e}_{y}\sin{\phi} \tag{6}
\end{align}
\(\phi\)で偏微分すると、
\begin{align}
\frac{\partial\boldsymbol{r}}{\partial \phi}=-\boldsymbol{e}_{x}r\sin{\phi}+\boldsymbol{e}_{y}r\cos{\phi} \tag{7}
\end{align}
最後に、(6)、(7)を規格化します。
\begin{align}
\boldsymbol{e}_{r}&\equiv\frac{\partial\boldsymbol{r}}{\partial r}\left/\left|\frac{\partial\boldsymbol{r}}{\partial r}\right|\right.=\cos{\phi}\boldsymbol{e}_{x}+\sin{\phi}\boldsymbol{e}_{y}, \tag{8}\\
\boldsymbol{e}_{\phi}&\equiv\frac{\partial\boldsymbol{r}}{\partial \phi}\left/\left|\frac{\partial\boldsymbol{r}}{\partial \phi}\right|\right.=-\sin{\phi}\boldsymbol{e}_{x}+\cos{\phi}\boldsymbol{e}_{y} \tag{2}
\end{align}
このようにして、2次元極座標の基底ベクトルが求められました!

