こんにちは!
この記事では、力学変数の定義とその具体例を紹介します!
なので次のような方に向けた記事となります!
- 力学変数の定義を知りたい
- その具体例を知りたい
早速内容に入りましょう(^^)
力学変数の定義
力学変数とは、ある時刻において物理系の状態を一意に決定するための変数の集まりです。
力学変数のことを、一般化座標ともいいます。
ニュートン力学では、例えば直交座標を\(\boldsymbol{r}(t)=(x(t),y(t),z(t))\)と表しました。
解析力学では、いわゆる座標以外も力学変数となりうるので、一般に力学変数を\(q_i(t)\)と表すことが多いです。
ただし、系の自由度が\(N\)のとき、\(i=1,\dots,N\)です。
(例えば、解析力学の枠組み(のある種の極限である場の理論)で電磁場を定式化することができ、その際は、スカラーポテンシャル\(\phi(\boldsymbol{r},t)\)とベクトルポテンシャル\(\boldsymbol{A}(\boldsymbol{r},t)\)が力学変数となります。ここではこれ以上触れませんが、後々記事にできたらいいなあ(^O^))
これから具体例を紹介します!
力学変数の例:1質点系
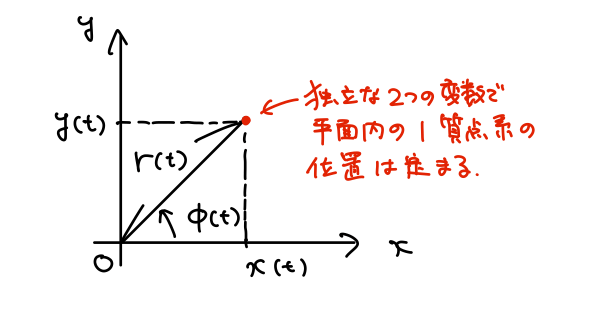
質点は大きさをもたない仮想的な物体なので、その位置が決まれば、ある時刻における状態が定まったことになります。
\(n\)次元空間中を運動する1質点系の自由度は\(N=n\)です。
例えば、\(N=n=2\)ならば平面内の運動なので、力学変数として直交座標\((q_1(t),q_2(t))=(x(t),y(t))\)や、極座標\((q_1(t),q_2(t))=(r(t),\phi(t))\)などと選ぶことができます。
力学変数の例:剛体
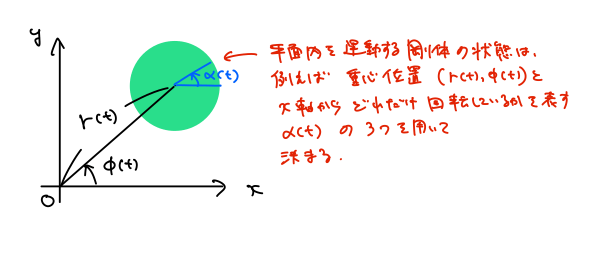
次に、2次元平面内を運動する剛体の自由度を考えてみましょう。
剛体の配位を指定するには、例えば、慣性系の座標と剛体にくっついた座標を定める必要があります。
図のように、慣性系の座標として重心の極座標\((q_1(t),q_2(t))=(r(t),\phi(t))\)、剛体にくっついた座標として\(q_3(t)=\alpha(t)\)をとることができます。
\(\alpha(t)\)は剛体が平面内でどれだけ回転しているかを表す力学変数です。
これらをまとめると、\((q_1(t),q_2(t),q_3(t))=(r(t),\phi(t),\alpha(t))\)となります。
また、3次元空間中の剛体を考える際は、重心座標とオイラー角をとることができます。
まとめ
力学変数の定義とその具体例について紹介しました!
力学変数とは、ある時刻において物理系の状態を一意に決定するための変数の集まりです。
それでは!


