こんにちは!
この記事では、微分と変分が可換であることを証明したいと思います。
例えば、解析力学で最小作用の原理からEuler-Lagrange方程式を導く際に、
\begin{align}
\delta \dot{q}(t)=\frac{d}{dt}\delta q(t) \tag{1}
\end{align}
という変形をします。
しかし、いろいろな解析力学の本をみても、この変形ができる理由は述べてくれませんでした(^^;)
なんで微分と変分って交換できるの?!
と思った方のなんと多いことでしょう(私だけですかね、、笑)
その理由をこれから説明します!(^^)
証明の準備:微分と変分の違い
まず、微分と変分の違いを明確にしましょう。
ここが重要です!!
微分
変数の変化に対する関数の変化率
変分
- 変数を変えない関数の任意の微小なずれ
- そのずれによって引き起こされる汎関数の変化分(この記事の目標から外れるのでこれについては書きません)
それぞれ数式と図を使って説明していきます。
変数\(t\)をもつ関数\(q(t)\)を考えます。(記号の使い方は解析力学を念頭に置いています)
微分の定義は、
\begin{align}
\frac{d}{dt}q(t)=\lim_{\Delta t\to0}\frac{q(t+\Delta t)-q(t)}{\Delta t} \tag{2}
\end{align}
です。
つまり、「変数を\(\Delta t\)だけずらしたとき、関数\(q(t)\)がどれだけ変化するか」を表す量が微分です。
図で表すと下のようになります。
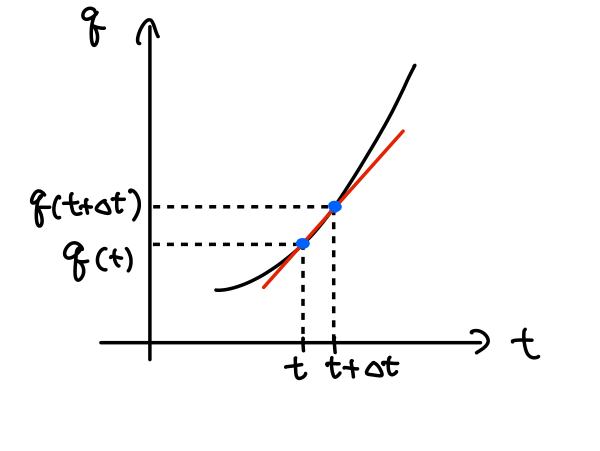
\(\Delta t\to0\)としたときの接線(赤線)の傾きが微分です。
次に、変分について説明します。
先ほど「変数を変えない関数の任意の微小なずれ」と説明しましたが、それを数式で表すと、
\begin{align}
q(t)+\delta q(t) \tag{3}
\end{align}
となります。
この(3)における\(\delta q(t)\)を\(q(t)\)の変分といいます。
図で表すと下のようになります。
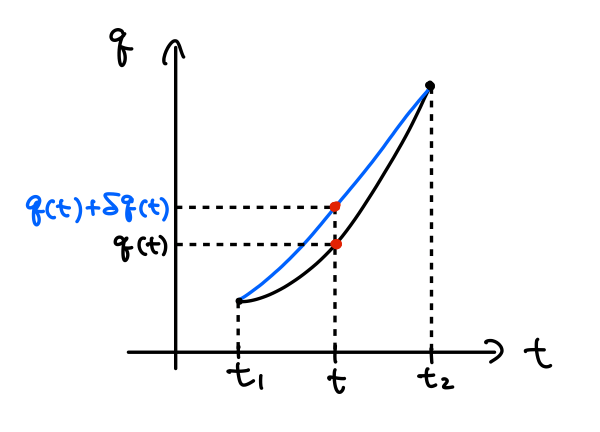
最小作用の原理を想定して、端点\(t=t_1,\,t_2\)で\(\delta q(t_1)=\delta q(t_2)=0\)としました。
ここで重要なことは、変分は変数を変えずに、各\(t\)に対して任意に選ぶことができる点です。
微分と変分が可換であることの証明
2つの関数\(q(t),\,\tilde{q}(t)\)を考えましょう。
ここで、\(\tilde{q}(t)=q(t)+\delta q(t)\)とします。
それでは、関数\(q(t)\)の微分の変分を考えましょう。
\begin{align}
\delta \frac{d}{dt}q(t)=\frac{d\tilde{q}(t)}{dt}-\frac{dq(t)}{dt}
\end{align}
ここでは、\(\frac{d}{dt}q(t)\)という関数の変分を取りました。
変分では変数\(t\)は変わらないので、第1項は\(t\)の微分です。
次に、微分の線形性により、
\begin{align}
\frac{d\tilde{q}(t)}{dt}-\frac{dq(t)}{dt}
&=\frac{d}{dt}\left(\tilde{q}(t)-q(t)\right)\\
&=\frac{d}{dt}\left(q(t)+\delta q(t)-q(t)\right)\\
&=\frac{d}{dt}\delta q(t)
\end{align}
2行目では、\(\tilde{q}(t)\)の定義を代入しました。
以上より、
\begin{align}
\delta \dot{q}(t)=\frac{d}{dt}\delta q(t) \tag{1}
\end{align}
となります。
まとめ
この記事では、微分と変分が可換であることを丁寧に証明してみました。
この変形のような、本には載ってないけど皆当たり前のように使う変形が、どうしてそうなるのかを理解できると嬉しいですよね!(^^)
そのような計算をこのブログで発信していって、物理を学ぶ方々の手助けができれば幸いです(^o^)
それでは!


