【力学】回転軸の選び方

こんにちは！

この記事では、\(n\)次元空間における回転軸の選び方が何通りあるのかを説明します！

この記事は次のような方におすすめです(^^)

短い記事なので、ぜひ最後までご覧ください！

２次元空間における回転軸の選び方

まず、２次元空間を考えましょう。

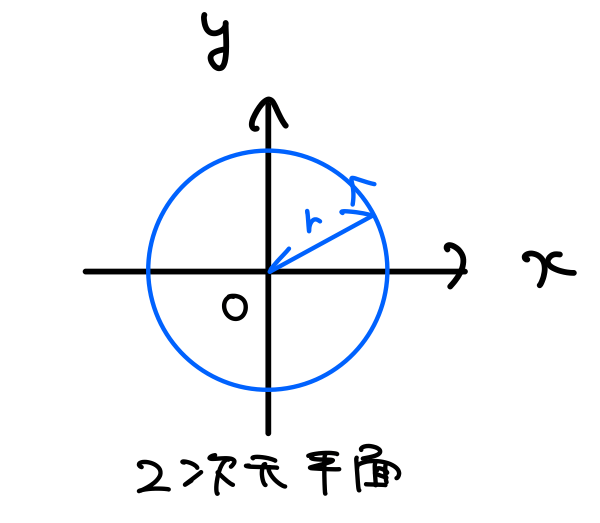
回転運動の１つとして、図のような原点を中心とした半径\(r \)の円運動が考えられます。

この回転はもちろん\(xy \)平面内であり、回転軸は\(z \)軸方向です。

明らかに回転軸の選び方はこの１通りです。

これをあえて\({}_2 \mathrm{C}_2=1\)とかいておきましょう。

３次元空間における回転軸の選び方

次に、３次元空間を考えましょう。

独立な回転運動として例えば、\(xy \)平面内、\(yz \)平面内、\(zx \)平面内の３通りをとることができます。

つまり、回転軸の選び方は３通りになります。

これをあえて\({}_3 \mathrm{C}_2=3\)とかいておきましょう。

\(n\)次元空間における回転軸の選び方

最後に、\(n\)次元空間を考えましょう。

もうお気づきの方もいるとは思いますが、\(n\)次元空間における回転軸の選び方は、\({}_n \mathrm{C}_2=n(n-1)/2\)となります。

その理由は、回転軸を指定するためには平面を決めれば良いからです。

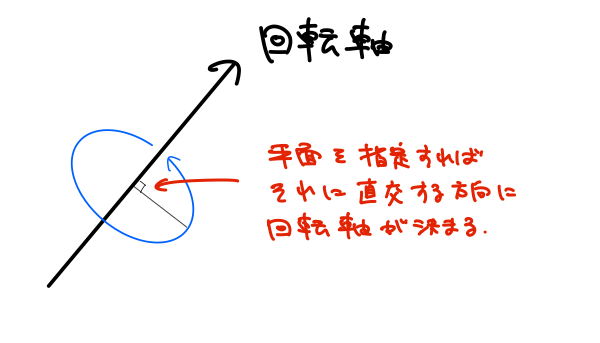
\(n \)次元空間なので、\(n \)個の方向から２つを選ぶと１つの平面ができます。

よって、独立な平面の数は\({}_n \mathrm{C}_2=n(n-1)/2\)となります。

まとめ

それでは！