こんにちは!
この記事では、コンプトン効果を解説します!
コンプトン効果とは?
コンプトン効果
自由電子にX線を投射したとき、散乱されたX線の波長が入射X線の波長よりも長くなる現象
また、コンプトン効果が現れる散乱を、コンプトン散乱といいます。
歴史的には、1905年にEinsteinが提唱した「光量子仮説」の裏付けとなる実験として有名です。
光量子仮説
光が波動的性質とともに粒子的性質をも合わせもつと考え、角振動数\(\omega\)、波数\(k\)の光(電磁波)は、エネルギー\(E=\hbar\omega\)、運動量\(p=\hbar k\)の光子の集まりであるとする
コンプトン波長
コンプトン散乱の計算をして、どれくらい波長が伸びるのかを調べます。
以下の図のような設定を考えます。
自由電子(質量\(m\))の静止系で、エネルギー\(\hbar\omega\)、運動量\(\hbar \boldsymbol{k}\)をもつ光子を入射させます。
そして、散乱角を\(\theta\)、散乱光子のエネルギーを\(\hbar\omega’\)、運動量を\(\hbar \boldsymbol{k}’\)、反跳電子の運動量を\(\boldsymbol{p}\)とします。
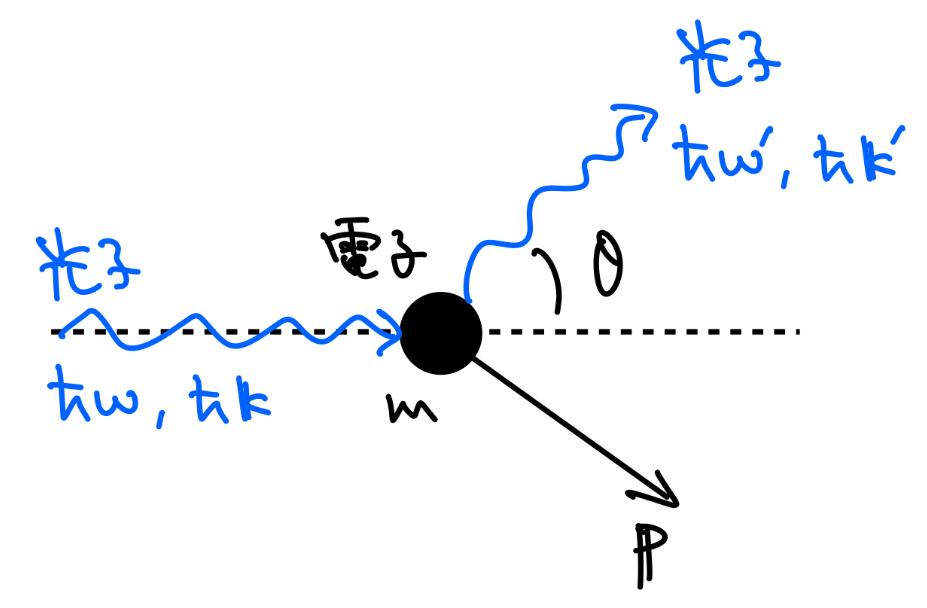
エネルギー・運動量保存則より、
\begin{align}
mc^2+\hbar\omega&=c\sqrt{\boldsymbol{p}^2+m^2c^2}+\hbar\omega’, \tag{1}\\
\hbar\boldsymbol{k}&=\hbar\boldsymbol{k}’+\boldsymbol{p} \tag{2}
\end{align}
が成り立ちます。
これらの式から\(\boldsymbol{p}\)を消去すると、
\begin{align}
\Delta\lambda\equiv\lambda’-\lambda=\frac{h}{mc}(1-\cos{\theta}) \tag{3}
\end{align}
が得られます。
これは散乱前後の波長の変化を表していて、散乱後に波長が伸びることがわかります。
ここで、\(\frac{h}{mc}\)をコンプトン波長といい、電子の質量\(m=0.511\,\rm MeV\)に対して、
\begin{align}
\frac{h}{mc}\simeq2.43\times10^{-12}\,\rm m \tag{4}
\end{align}
となります。
量子論の基本定数であるプランク定数\(h\)と相対論の基本定数である光速\(c\)を用いて電子の質量を長さに変換しており、これは電子の世界の特徴的な長さスケールとなっています。


