【ベクトル解析】発散（div）の定義、物理的意味、具体的なイメージ

こんにちは！

以前、勾配（grad）の定義、物理的意味、具体的なイメージを解説した記事を挙げました！

図を用いてわかりやすく説明しているので、興味のある方はこちらからどうぞ(^^)

さて、勾配の次に我々に立ちはだかる概念が、「発散」です。

「新しい概念がいっぱい出てきて頭が発散しそう～(T-T)」という方もこの記事を読めば「え、発散？私がわかりやすく説明してあげよう(☆｡☆)」となるでしょう笑

早速内容に入りましょう！

発散（div）の定義

ナブラ演算子とベクトル場の内積で書かれているので、発散はスカラーです。

発散は英語でdivergenceというので、その一部を取ってdivとも表します。

発散の物理的意味

どうして式(1)のことを発散というのでしょうか？

その理由を図を用いてわかりやすく説明していきます！

下図に示すような小さな直方体を考えます。

各辺の長さをそれぞれ\(\Delta x,\,\Delta y,\,\Delta z\)とします。

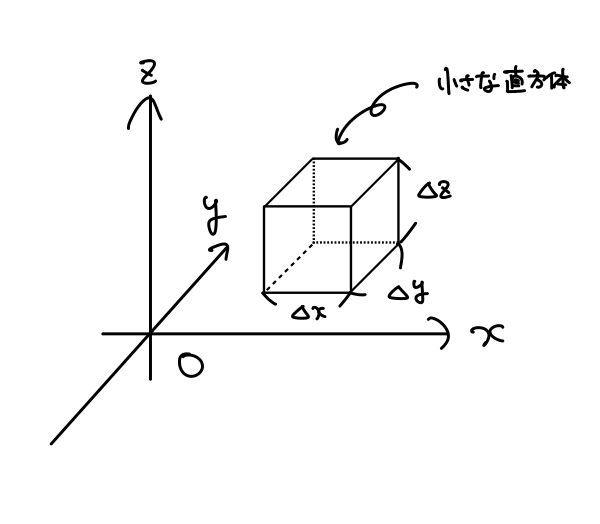
ベクトル場\(\boldsymbol{A}(\boldsymbol{r})\)がこの小さな直方体から流出する量を数式で表してみましょう。

下図のように、ベクトル場\(\boldsymbol{A}(\boldsymbol{r})\)は空間の各点にベクトル（矢印）がいる様子として図示できます。（川を流れる水の速度が場所によって異なるイメージです）

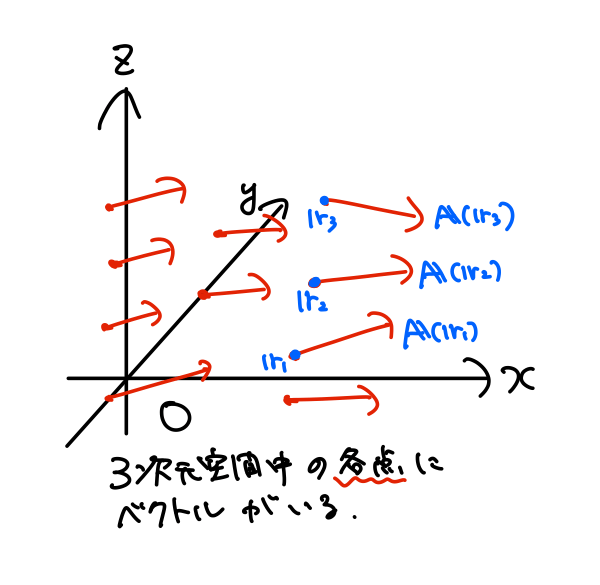
簡単のために、\(x \)方向のみを考えます。

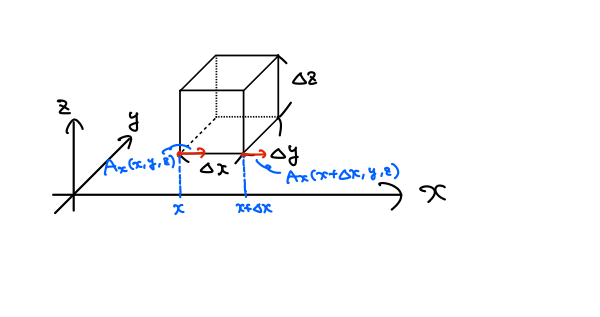
図のように、手前の角の２点における\(x \)方向の流出量を考えると、

\begin{align}
A_x(x+\Delta x,y,z)\Delta y\Delta z-A_x(x,y,z)\Delta y\Delta z
\end{align}

となります。

\(x=\text{一定}\)の面から流出するすべての量を、(その面の角の１点のベクトル場)\(\times\)(面積\(\Delta y\Delta z \))で表しています。また、第２項のマイナスは、\((x,y,z) \)においてベクトル場が流入しているので、それを反映しました。

\(y,\,z \)方向も同様なので、全流出量は次のようになります。

\begin{align}
A_x(x+\Delta x,y,z)\Delta y\Delta z-A_x(x,y,z)\Delta y\Delta z\\
+A_y(x,y+\Delta y,z)\Delta z\Delta x-A_y(x,y,z)\Delta z\Delta x\\
+A_z(x,y,z+\Delta z)\Delta x\Delta y-A_z(x,y,z)\Delta x\Delta y\\
\end{align}

\(\Delta x\Delta y\Delta z \)でくくると、

\begin{align}
\left(\frac{A_x(x+\Delta x,y,z)-A_x(x,y,z)}{\Delta x}
+\frac{A_y(x,y+\Delta y,z)-A_y(x,y,z)}{\Delta y}\right.\\
\left.+\frac{A_z(x,y,z+\Delta z)-A_z(x,y,z)}{\Delta z}\right)\Delta x\Delta y\Delta z
\end{align}

あと少しです！

\(\Delta x,\,\Delta y,\,\Delta z \to 0\)の極限を取りましょう。

\begin{align}
\left(\frac{\partial A_x(\boldsymbol{r})}{\partial x}+\frac{\partial A_y(\boldsymbol{r})}{\partial y}+\frac{\partial A_z(\boldsymbol{r})}{\partial z}\right)dxdydz
=\nabla\cdot\boldsymbol{A}(\boldsymbol{r})
\end{align}

となり、これは発散の定義そのものです！！(^^)

具体的なイメージ

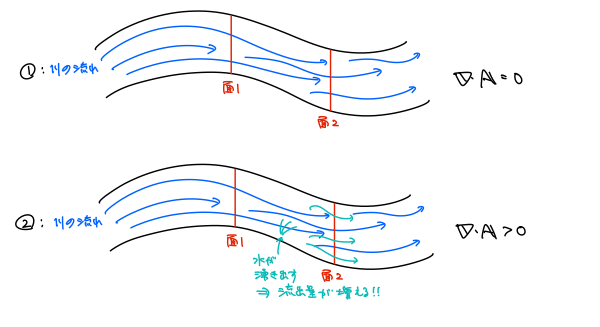
川を流れる水をイメージしましょう。

図の①の場合、面１から流入する量と面２から流出する量は直感的に等しいですよね。実際にこのような場合、

\begin{align}
\nabla\cdot\boldsymbol{A}(\boldsymbol{r})=0
\end{align}

となります。

これを湧き出しなしといいます。

一方で、図の②の場合、面１と面２の間から水が湧き出しています。

このとき、直感的に面１の流入量より面２の流出量が大きくなることがわかると思います。

つまり、

\begin{align}
\nabla\cdot\boldsymbol{A}(\boldsymbol{r})>0
\end{align}

となります。

まとめ

この記事では、発散の定義、物理的意味、具体的なイメージを説明しました。

簡単にまとめると、以下のようになります。

それでは！