こんにちは!
この記事では、ベクトル解析で出てくる勾配(gradient)という概念について説明します!
\({\rm{grad}} f\)?\(\nabla f\)?なにそれおいしいの?となっている方の参考になれば幸いです!
勾配の定義から物理的意味、具体的なイメージまで、図を用いてわかりやすく説明するので、ぜひ最後までお付き合いください!
勾配の定義
スカラー場\(f(\boldsymbol{r})\)を考えましょう。引数の\(\boldsymbol{r}\)は、\(\boldsymbol{r}=(x,y,z)\)のことです。
\(f(\boldsymbol{r})\)の全微分\(df(\boldsymbol{r})\)を次のように書きます。
\begin{align}
df(\boldsymbol{r})=f(\boldsymbol{r}+d\boldsymbol{r})-f(\boldsymbol{r})=(\nabla{f(\boldsymbol{r})})\cdot d\boldsymbol{r} \tag{1}
\end{align}
右辺の\(\nabla{f(\boldsymbol{r})}\)をスカラー場\(f(\boldsymbol{r})\)の勾配といいます。
\(\nabla{f(\boldsymbol{r})}\)のことを\({\rm{grad}} f(\boldsymbol{r})\)とかくときもあります。勾配を英語でgradientというので、これはその一部です。
また、\(\nabla\)のことをナブラ演算子といいます。
\(d\boldsymbol{r}\)というベクトルと内積をとって、\(df(\boldsymbol{r})\)というスカラーをつくるので、勾配はベクトルです。
直交座標系における勾配
直交座標系における勾配は次のようになります。
直交座標系における勾配
\begin{align}
\nabla{f(\boldsymbol{r})}=\boldsymbol{e}_x\frac{\partial f(\boldsymbol{r})}{\partial x}+\boldsymbol{e}_y\frac{\partial f(\boldsymbol{r})}{\partial y}+\boldsymbol{e}_z\frac{\partial f(\boldsymbol{r})}{\partial z} \tag{2}
\end{align}
これを確かめましょう。
まず、勾配の定義(1)に出てくる量を直交座標系で表します。
\begin{align}
df(\boldsymbol{r})
&=f(\boldsymbol{r}+d\boldsymbol{r})-f(\boldsymbol{r})\\
&=\frac{\partial f(\boldsymbol{r})}{\partial x}dx+\frac{\partial f(\boldsymbol{r})}{\partial y}dy+\frac{\partial f(\boldsymbol{r})}{\partial z}dz \tag{3}\\
d\boldsymbol{r}
&=\boldsymbol{e}_xdx+\boldsymbol{e}_ydy+\boldsymbol{e}_zdz \tag{4}
\end{align}
ここで、微小量の1次まで残しました。
実際に(2)と(4)の内積をとると(3)になることがわかるので、これで確かめられました。
直交座標系におけるナブラ演算子\(\nabla\)は、(2)から\(f(\boldsymbol{r})\)を取り除いて、
\begin{align}
\nabla=\boldsymbol{e}_x\frac{\partial}{\partial x}+\boldsymbol{e}_y\frac{\partial}{\partial y}+\boldsymbol{e}_z\frac{\partial}{\partial z} \tag{2}
\end{align}
と表されます。
勾配の物理的意味
ここから勾配の物理的意味を理解していきましょう!
勾配はベクトルなので、その大きさと向きについて考えます。
具体的に地図の等高線を用いて考えます。このとき、スカラー場\(f(\boldsymbol{r})\)は場所\(\boldsymbol{r}\)における標高を表します。
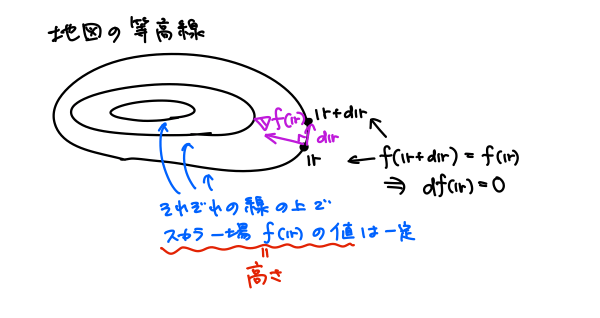
まず、向きから。
もちろん、1つの等高線上の任意の場所で、\(f(\boldsymbol{r})\)の値は変わりません。
したがって、\(d\boldsymbol{r}\)の向きを等高線に沿った方向にとると、
\begin{align}
df(\boldsymbol{r})=f(\boldsymbol{r}+d\boldsymbol{r})-f(\boldsymbol{r})=0 \tag{3}
\end{align}
となります。
よって、勾配\(\nabla{f(\boldsymbol{r})}\)と\(d\boldsymbol{r}\)は直交しており、\(\nabla{f(\boldsymbol{r})}\)は等高線に対して垂直な方向を向いています。
次に、大きさです。
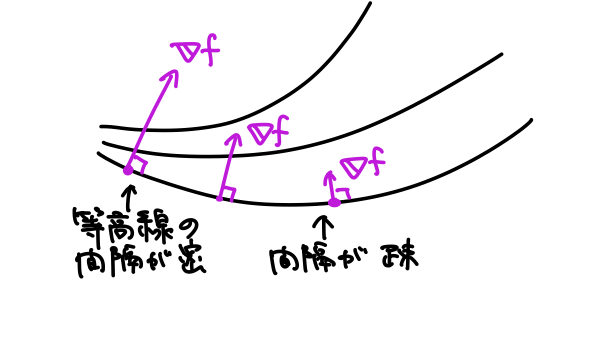
\(d\boldsymbol{r}\)の向きを任意とすると、
\begin{align}
df(\boldsymbol{r})=(\nabla{f(\boldsymbol{r})})\cdot d\boldsymbol{r}=|\nabla{f(\boldsymbol{r})}||d\boldsymbol{r}|\cos{\theta} \tag{4}
\end{align}
ここで、\(\theta\)は\(\nabla{f(\boldsymbol{r})}\)と\(d\boldsymbol{r}\)とのなす角です。
特定の位置\(\boldsymbol{r}\)に対して、\(\theta=0\)で\(df(\boldsymbol{r})\)が最大値をとるので、等高線に対して垂直な方向は最も標高の変化が大きいことがわかります。
\(|d\boldsymbol{r}|=\text{一定}\)のもとで、\(|\nabla{f(\boldsymbol{r})}|\propto df(\boldsymbol{r})\)なので、等高線の間隔が密であればあるほど、\(|\nabla{f(\boldsymbol{r})}|\)は大きくなります。
具体的なイメージ
物理で勾配が出てくる場面は、例えば、重力やクーロン力などの保存力とポテンシャルの関係を議論するときです。
しかし、ここでは具体的なイメージを持ってもらいたいので、これらについては触れずに簡単に説明します。
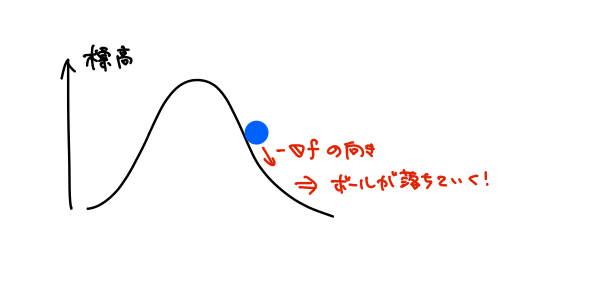
でこぼこしていない理想的な山の斜面にボールが置かれたとしましょう。
\(-\nabla{f(\boldsymbol{r})}\)は、位置\(\boldsymbol{r}\)にあるボールがどの方向に落ちやすいか(地面がどの方向に一番傾いているか)を特徴づけるベクトル量です。
ここで、勾配そのものは標高が「増える」向きを向いているので、勾配をマイナス倍すると、直感的にボールが落ちる向きを向きます。
日常的に使う「勾配」と同様の意味であることがわかると思います!
まとめ
この記事では、勾配の定義、物理的意味、具体的なイメージを説明しました。
簡単にまとめると、以下のようになります。
勾配の定義
\begin{align}
df(\boldsymbol{r})=(\nabla{f(\boldsymbol{r})})\cdot d\boldsymbol{r}
\end{align}
を満たす\(\nabla{f(\boldsymbol{r})}\)をスカラー場\(f(\boldsymbol{r})\)の勾配といいます。
物理的意味
\(\nabla{f(\boldsymbol{r})}\)は等高線に対して垂直な向きで、標高が高くなる方向を向くベクトルです。その大きさは、等高線の間隔が密であるほど大きくなります。
具体的なイメージ
山の斜面に置いたボールが転がっていくとき、その転がりやすさを表すベクトル量です。
勾配のほかに、発散と回転という概念もあるので、それらについても同様の記事を出せればと思っています!
それでは!


