【ベクトル解析】回転（rot）の定義、物理的意味、具体的なイメージ

こんにちは！

以前、勾配（grad）と発散（div）の定義、物理的意味、具体的なイメージを解説した記事を挙げました！

図を用いてわかりやすく説明しているので、興味のある方は以下のボタンからどうぞ(^^)（新たなタブが開きます）

「新しい概念がいっぱい出てきて頭が発散しそう～(T-T)」という方もこの記事を読めば「え、回転？私がわかりやすく説明してあげよう(☆｡☆)」となるでしょう笑

早速内容に入りましょう！

回転（rot）の定義

ナブラ演算子とベクトル場の外積で書かれているので、回転はベクトルです。

回転は英語でrotationというので、その一部を取ってrotとも表します。

ちなみに、回転をcurlともいうので、rotではなくcurlとかいている本もあります。

回転の物理的意味

簡単のため、２次元ベクトル場\(\boldsymbol{A}(\boldsymbol{r})=\boldsymbol{e}_xA_x(\boldsymbol{r})+\boldsymbol{e}_yA_y(\boldsymbol{r})\)に対する回転

\begin{align}
\nabla\times\boldsymbol{A}(\boldsymbol{r})=\boldsymbol{e}_z\left(\frac{\partial A_y(\boldsymbol{r})}{\partial x}-\frac{\partial A_x(\boldsymbol{r})}{\partial y}\right)
\end{align}

について考えましょう。

ここで、\(\boldsymbol{r}=(x,y)\)です。

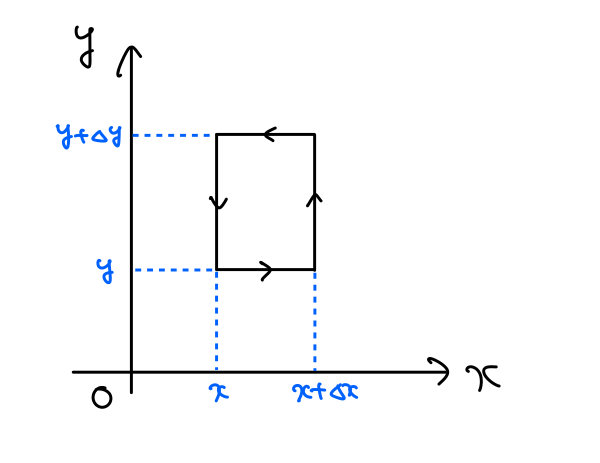
図のように、\(xy \)平面上で各辺が座標軸に平行な微小長方形を考えます。長方形の辺に沿って反時計回りの方向を正とします。

この経路に沿ったベクトル場\(\boldsymbol{A}(\boldsymbol{r})\)の流量は、

\begin{align}
&A_x(x,y)\Delta x-A_x(x,y+\Delta y)\Delta x+A_y(x+\Delta x,y)\Delta y-A_y(x,y)\Delta y\\
&=\left(\frac{A_y(x+\Delta x,y)-A_y(x,y)}{\Delta x}-\frac{A_x(x,y+\Delta y)-A_x(x,y)}{\Delta y}\right)\Delta x\Delta y
\end{align}

となります。

ここで、図の矢印と座標軸の向きが同じであればプラス、逆向きであればマイナスの符号になることに注意しましょう！

\(\Delta x,\,\Delta y\to0\)の極限をとると、

\begin{align}
\left(\frac{\partial A_y(\boldsymbol{r})}{\partial x}-\frac{\partial A_x(\boldsymbol{r})}{\partial y}\right)dxdy
\end{align}

となります。ベクトル場の回転の表式が出てきました！！(^^)

よって、\(\left(\frac{\partial A_y(\boldsymbol{r})}{\partial x}-\frac{\partial A_x(\boldsymbol{r})}{\partial y}\right)\)は、位置\(\boldsymbol{r}\)における回転の強さを表す量と解釈できます。

さらに、\(xy \)平面上の回転を表す回転軸は\(z \)軸になります。これが回転を特徴づける方向です！

回転軸の選び方については、こちらを参照してください！

したがって、位置\(\boldsymbol{r}\)における回転を特徴づける量として

\begin{align}
\nabla\times\boldsymbol{A}(\boldsymbol{r})=\boldsymbol{e}_z\left(\frac{\partial A_y(\boldsymbol{r})}{\partial x}-\frac{\partial A_x(\boldsymbol{r})}{\partial y}\right)
\end{align}

が得られます！

具体的なイメージ

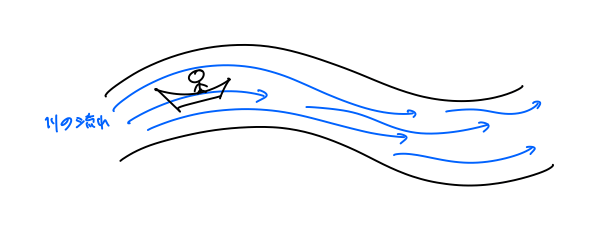
図のように筏いかだで川下りをしているとしましょう。

理想的な川としてまっすぐな川を考えると、川の流れが一様であれば、筏は回転することなく明らかにまっすぐ移動します。

一方で、もちろん川の流れは場所によって異なるので、一様でなければ図のように筏が回転することも想像できるでしょう。

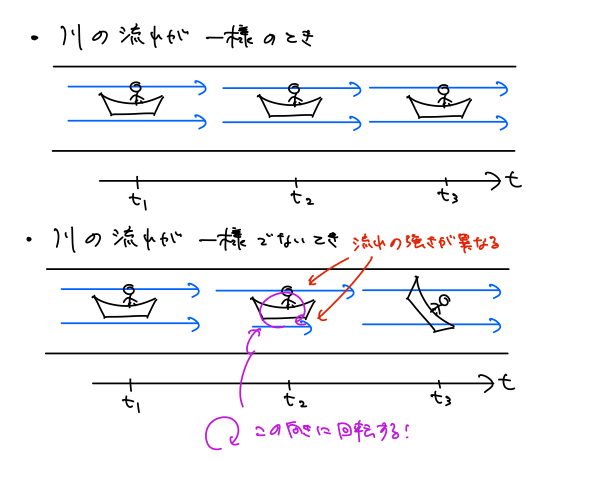
このときの筏を回転させる量が、ベクトル場の回転です。（いま、ベクトル場は水の流れです。）

まとめ

この記事では、回転の定義、物理的意味、具体的なイメージを説明しました。

簡単にまとめると、以下のようになります。

それでは！