こんにちは!
数学や物理を学んでいるときに、次のような悩みはありませんか?
- 2次元ベクトルや3次元ベクトルの内積や外積の計算はできるけど、いちいち全部の式を書くのが面倒臭い!
- クロネッカーデルタ\(\delta_{ij}\)、レビチビタ記号\(\epsilon_{ijk}\)って何??
- 物理の本を読んでいて、和の記号\(\sum\)が書いてない!これって誤植??
このような悩みをもっている人も多いと思います。
この記事では、これらの疑問を解決する手助けができればと思います!!
早速内容に入りましょう!(^^)
3次元ベクトルの内積と外積
まず、3次元ベクトルの内積と外積について復習しましょう。
\(\boldsymbol{a}\)と\(\boldsymbol{b}\)を次の3次元ベクトルとします。
\begin{align}
\boldsymbol{a}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix},\quad
\boldsymbol{b}=\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} \tag{1}
\end{align}
これらに対して、ベクトルの内積と外積は次のように定義されます。
\begin{align}
&\text{内積}\quad\boldsymbol{a}\cdot\boldsymbol{b}=a_1b_1+a_2b_2+a_3b_3 \tag{2}\\
&\text{外積}\quad\boldsymbol{a}\times\boldsymbol{b}=\boldsymbol{e}_1(a_2b_3-a_3b_2)+\boldsymbol{e}_2(a_3b_1-a_1b_3)+\boldsymbol{e}_3(a_1b_2-a_2b_1) \tag{3}
\end{align}
ここで、
\begin{align}
\boldsymbol{e}_1=\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix},\quad
\boldsymbol{e}_2=\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix},\quad
\boldsymbol{e}_3=\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \tag{4}
\end{align}
です。これらは3次元直交座標系における正規直交基底です。
クロネッカーデルタを用いた内積の記法
上で与えた内積の式(2)をクロネッカーデルタ\(\delta_{ij}\)を用いて書き換えましょう。
クロネッカーデルタの定義は次の通りです。
クロネッカーデルタの定義
\begin{align}
\delta_{ij}=
\begin{cases}
1\quad(i=j)\\
0\quad(i\neq j)
\end{cases} \tag{5}
\end{align}
\(i,\,j\)にはそれぞれ\(1,\,2,\,3\)のどれかが入ります。
例えば、\(\delta_{11}=1\)、\(\delta_{23}=0\)、\(\delta_{21}=0\)などとなります。
すなわち、2つの添字が同じであれば1、異なれば0となる記号です。
ここで、改めて内積(2)を見てみましょう。
\begin{align}
&\text{内積}\quad\boldsymbol{a}\cdot\boldsymbol{b}=a_1b_1+a_2b_2+a_3b_3
\end{align}
右辺の各項の添字がそれぞれ同じになっています!
よって、この式を
\begin{align}
&\text{内積}\quad\boldsymbol{a}\cdot\boldsymbol{b}=a_1b_1+a_2b_2+a_3b_3=\sum_{i,j=1}^3a_i\delta_{ij}b_j=\sum_{i=1}^3a_ib_i \tag{6}
\end{align}
と書き換えることができます。
レビチビタ記号を用いた外積の記法
次に、外積(3)をレビチビタ記号\(\epsilon_{ijk}\)を用いて表しましょう。
レビチビタ記号の定義は次の通りです。
レビチビタ記号の定義
\begin{align}
\epsilon_{123}=1,\quad\epsilon_{ijk}=\epsilon_{jki}=\epsilon_{kij}=-\epsilon_{ikj}\quad(i,j,k=1,2,3) \tag{7}
\end{align}
右側の条件は、レビチビタ記号が添字\(i,\,j,\,k\)の入れ替えに関して完全反対称であるということを意味しています。
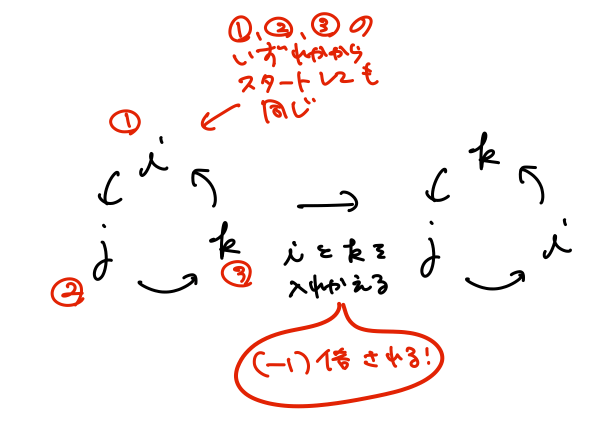
すなわち、図のように、3つの添字の並び順は変えずに(一般には偶数回変えて)、どこからスタートするかを変えても、符号は変わらない。また、並び順を1回変えると(一般には奇数回変えると)、符号が変わる(\(-1\)倍される)。
ということです。
\(\epsilon_{123}=1\)と定義したので、例えば、\(\epsilon_{231}=\epsilon_{312}=1,\,\epsilon_{132}=-1,\,\epsilon_{113}=0\)となります。
さて、レビチビタ記号の導入ができたので、外積(3)を書き換えましょう。
その結果は、
\begin{align}
\boldsymbol{a}\times\boldsymbol{b}&=\boldsymbol{e}_1(a_2b_3-a_3b_2)+\boldsymbol{e}_2(a_3b_1-a_1b_3)+\boldsymbol{e}_3(a_1b_2-a_2b_1)\\ &=\sum_{i,j,k=1}^3\boldsymbol{e}_i\epsilon_{ijk}a_jb_k \tag{8}
\end{align}
となります。
例えば、\(\boldsymbol{e}_1\)の成分を全て書き出すと、
\begin{align}
\sum_{j,k=1}^3\epsilon_{1jk}a_jb_k
&=\epsilon_{111}a_1b_1+\epsilon_{122}a_2b_2+\epsilon_{133}a_3b_3\\
&\quad+\epsilon_{112}a_1b_2+\epsilon_{113k}a_1b_3+\epsilon_{123}a_2b_3\\
&\quad+\epsilon_{121}a_2b_1+\epsilon_{131}a_3b_1+\epsilon_{132}a_3b_2 \tag{9}
\end{align}
2行目の第3項と3行目の第3項だけが残り、他の項はそれぞれゼロになります。
よって、
\begin{align}
\sum_{j,k=1}^3\epsilon_{1jk}a_jb_k
&=\epsilon_{123}a_2b_3+\epsilon_{132}a_3b_2=a_2b_3-a_3b_2 \tag{10}
\end{align}
となり、正しそうです。
同様にして、\(\boldsymbol{e}_2\)と\(\boldsymbol{e}_3\)の成分に対しても、正しいことがわかります。
アインシュタインの規約
最後に、アインシュタインの規約(縮約などともいいます)について説明しましょう。
アインシュタインの規約
式の中に同じ添字が2回出てきた場合、\(\sum\)を省略した上で、その添字について適当な和をとるものとする
具体例を見ましょう。
先ほど計算した、内積の式を見てみます。
\begin{align}
\boldsymbol{a}\cdot\boldsymbol{b}=\sum_{i=1}^3a_ib_i
\end{align}
右辺に\(i\)という添字が2回出てきています!なので、アインシュタインの規約に則り、
\begin{align}
\boldsymbol{a}\cdot\boldsymbol{b}=a_ib_i \tag{11}
\end{align}
と表記します。
同様に、外積に対しても、\(i,\,j,\,k\)という添字がそれぞれ2回出てきているので、
\begin{align}
\boldsymbol{a}\times\boldsymbol{b}=\boldsymbol{e}_i\epsilon_{ijk}a_jb_k \tag{12}
\end{align}
と表記します。
このような規則のことをアインシュタインの規約といいます。
まとめ
3次元ベクトルの内積および外積の表式は、
\begin{align}
\text{内積}\quad\boldsymbol{a}\cdot\boldsymbol{b}&=a_1b_1+a_2b_2+a_3b_3=\sum_{i=1}^3a_ib_i=a_ib_i\\
\text{外積}\quad\boldsymbol{a}\times\boldsymbol{b}
&=\boldsymbol{e}_1(a_2b_3-a_3b_2)+\boldsymbol{e}_2(a_3b_1-a_1b_3)+\boldsymbol{e}_3(a_1b_2-a_2b_1)\\
&=\sum_{i,j,k=1}^3\boldsymbol{e}_i\epsilon_{ijk}a_jb_k=\boldsymbol{e}_i\epsilon_{ijk}a_jb_k
\end{align}
です。最後の等式では、アインシュタインの規約を用いて、\(\sum\)を省略しました。
この記事がみなさんの学習のサポートになれば幸いです!
それでは!


