こんにちは!
この記事は、次のような方におすすめです!
- 球面調和関数の定義や性質を確認したい
早速内容に入りましょう!(^^)
定義
\(0\le\theta\le\pi,\,0\le\phi\le2\pi\)として、球面調和関数\(Y_{lm}(\theta,\phi)\)を次で定義します:
\begin{align}
Y_{lm}(\theta,\phi)\equiv(-1)^m\sqrt{\frac{2l+1}{4\pi}\frac{(l-m)!}{(l+m)!}}P_l^{\,m}(\cos{\theta})e^{im\phi} \tag{1}
\end{align}
ただし、\(P_l^{\,m}(\cos{\theta})\)はルジャンドル陪関数で、\(l=0,1,2,\dots;m=-l,-l+1,\dots,l-1,l\)です。
ルジャンドル陪関数についてはこちらの記事をご覧ください(定義や性質などがまとまっています!\(m\)の範囲がこうなる理由も説明してます(^^))
l=0,1に対する球面調和関数
\(l=0\)のとき、\(m\)の取り得る範囲は\(m=0\)で、
\begin{align}
Y_{00}=\sqrt{\frac{1}{4\pi}} \tag{2}
\end{align}
\(l=1\)のとき、\(m\)の取り得る範囲は\(m=-1,0,1\)で、
\begin{align}
Y_{11}&=-\sqrt{\frac{3}{8\pi}} \tag{3}\\
Y_{10}&=\sqrt{\frac{3}{4\pi}}\cos{\theta} \tag{4}\\
Y_{1,-1}&=\sqrt{\frac{3}{8\pi}}\sin{\theta}e^{-i\phi} \tag{5}
\end{align}
複素共役
\begin{align}
Y_{lm}(\theta,\phi)^\ast=(-1)^mY_{l,-m}(\theta,\phi) \tag{6}
\end{align}
空間反転
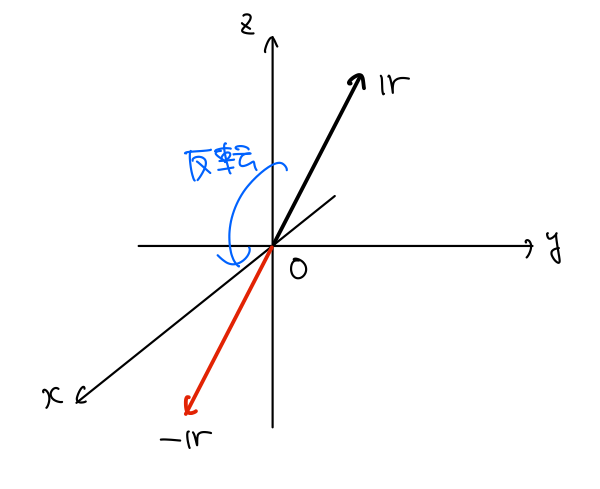
まず、極座標系において座標変換\((r,\theta,\phi)\to(r,\pi-\theta,\phi+\pi)\)が空間反転を表していることを説明します。
\begin{align}
x&=r\sin{\theta}\cos{\phi}\\
&\to r\sin{(\pi-\theta)}\cos{(\phi+\pi)}=-r\sin{\theta}\cos{\phi}=-x \tag{7}\\
y&=r\sin{\theta}\sin{\phi}\\
&\to r\sin{(\pi-\theta)}\sin{(\phi+\pi)}=-r\sin{\theta}\sin{\phi}=-y \tag{8}\\
z&=r\cos{\theta}\\
&\to r\cos{(\pi-\theta)}=-r\cos{\theta}=-z \tag{9}
\end{align}
よって、位置ベクトル\(\boldsymbol{r}=(x,y,z)\)はこの変換で、
\begin{align}
\boldsymbol{r}=(x,y,z)\quad\to\quad-\boldsymbol{r}=-(x,y,z) \tag{10}
\end{align}
となり、これは空間反転を表しています。
この変換の前後の球面調和関数は次の関係を満たします:
\begin{align}
Y_{lm}(\pi-\theta,\phi+\pi)=(-1)^lY_{lm}(\theta,\phi) \tag{11}
\end{align}
漸化式
\begin{align}
e^{i\phi}\left(\frac{\partial}{\partial \theta}+i\cot{\theta}\frac{\partial}{\partial \phi}\right)Y_{lm}(\theta,\phi)&=\sqrt{(l-m)(l+m+1)}Y_{l,m+1}(\theta,\phi) \tag{12}\\
e^{-i\phi}\left(-\frac{\partial}{\partial \theta}+i\cot{\theta}\frac{\partial}{\partial \phi}\right)Y_{lm}(\theta,\phi)&=\sqrt{(l+m)(l-m+1)}Y_{l,m-1}(\theta,\phi) \tag{13}
\end{align}
これは量子力学で重要な関係式です(昇降演算子)。
微分方程式
\begin{align}
\left[\frac{\partial^2}{\partial \theta^2}+\cot{\theta}\frac{\partial}{\partial \theta}+\frac{1}{\sin^2{\theta}}\frac{\partial^2}{\partial \phi^2}+l(l+1)\right]Y_{lm}(\theta,\phi)=0 \tag{14}
\end{align}
直交性
\begin{align}
\int^\pi_0d\theta\,\sin{\theta}\int^{2\pi}_0d\phi\,Y_{lm}(\theta,\phi)^\ast Y_{l’m’}(\theta,\phi)=\delta_{ll’}\delta_{mm’} \tag{15}
\end{align}
完全性
\begin{align}
\sin{\theta’}\sum_{l=0}^\infty\sum_{m=-l}^{l}Y_{lm}(\theta,\phi)Y_{lm}(\theta’,\phi’)^\ast=\delta(\theta-\theta’)\delta(\phi-\phi’) \tag{16}
\end{align}
加法定理
\begin{align}
P_l(\cos{\alpha})=\frac{4\pi}{2l+1}\sum_{m=-l}^lY_{lm}(\theta_1,\phi_1)Y_{lm}(\theta_2,\phi_2)^\ast \tag{17}
\end{align}
ここで、\(P_l\)はルジャンドル多項式で、
\begin{align}
\cos{\alpha}=\cos{\theta_1}\cos{\theta_2}+\sin{\theta_1}\sin{\theta_2}\cos{(\phi_1-\phi_2)} \tag{18}
\end{align}
ルジャンドル多項式について詳しくは、こちらの記事をご覧ください!↓


