こんにちは!
力学を学び終えた学生たちに立ちはだかる次なる壁。。。その名は解析力学!!
解析力学?力学を学んだから十分じゃないの?何に使うの?と思う人もいると思います。
この記事では、力学を学び終えて、これから解析力学を学ぼうとする物理系学生に向けて、なぜ解析力学を学ぶのかを説明します!
解析力学を学ぶモチベーションアップにつながれば嬉しいです!(^^)
解析力学を学ぶ理由:ニュートン力学の再定式化
解析力学を学ぶ理由の1つとして、ニュートン力学の再定式化が挙げられます。
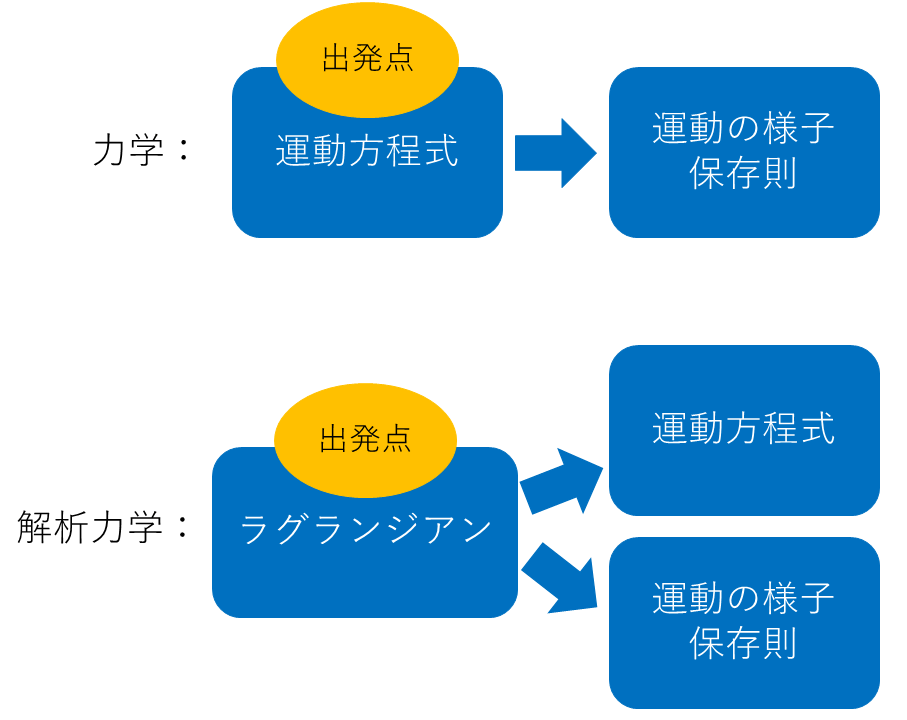
図のように、ニュートン力学では、理論の出発点は運動方程式(運動の3法則)です。
なので、運動方程式を書き下して、それを解くことで運動の様子を理解したり、運動量保存則やエネルギー保存則といった保存則を導きます。
一方で、解析力学では、ラグランジアン\(L\)という量が理論の出発点となります。(書きながら最小作用の原理か?と思いましたが、一旦スルーします笑。)
ここで詳しい議論はしませんが、だいたい\(L=T-U\)です。
ここで、\(T\)は運動エネルギー、\(U\)はポテンシャルです。
このラグランジアンから、運動方程式を導出したり、保存則を理解したりできます。
なぜこれでニュートン力学の再定式化になっているかというと、
ラグランジアンから次のような座標系に依らない形で運動方程式が得られるからです。
\begin{align}
\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}}\right)-\frac{\partial L}{\partial q}=0
\end{align}
ここで、\(q\)は一般化座標、\(\dot{q}=\frac{dq}{dt}\)です。
一般化座標というのは、例えば、直交座標系の\(x\)、極座標系の\(r\)、\(\phi\)などのことです。(詳しくはこちらをご覧ください!)
力学を学ぶと、直交座標系の運動方程式や極座標系の運動方程式などが出てきて、覚えるのに苦労したという人もいるかもしれません。
そのような方も安心してください!
解析力学を学べば、それらの式を覚える必要はなくなります!!ラグランジアンを微分すると勝手にでてきます笑
また、ラグランジアンの表式がわかれば、運動方程式を求めなくても、保存量がわかります。
保存量は運動を特徴づける量なので、これである程度運動の様子がわかるということです。
話は少し飛躍しますが、この事実は、相対性理論や素粒子物理学などを学ぶ際にも重要になってきます!
そのため、特に宇宙や素粒子に興味を持って物理を学んでいる人にとって、解析力学は必修科目です!
他の理由
詳しくは述べませんが、解析力学を勉強すると、次のような利点もあります。
- 量子力学の勉強にスムーズに進みやすくなる(ハミルトニアン、ポアソン括弧と交換関係、など)
- 電磁気学や相対性理論などの理解が深まる(最小作用の原理、正準運動量、など)
- 素粒子論、宇宙論、弦理論などの最先端に触れるために必要な場の理論につながる(いつか記事を書きたい…!!)
まとめ
今回は、解析力学を学ぶ理由について、数式をあまり使わずに説明してみました。
この記事が解析力学を学ぶモチベーションアップにつながれば嬉しいです(^o^)
解析力学は奥が深く、まだまだ勉強不足だと思っているので、気づいたことがあればその都度記事にして共有していきたいと思います!
それでは!


